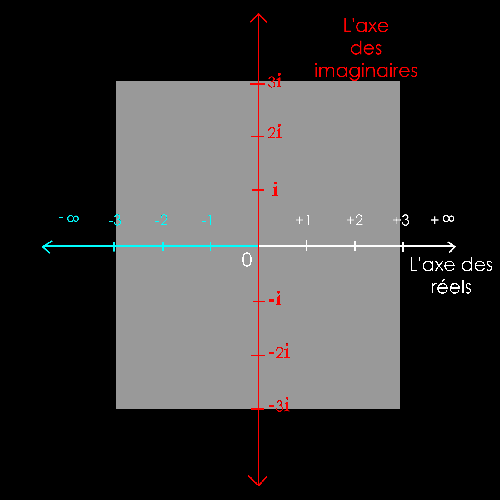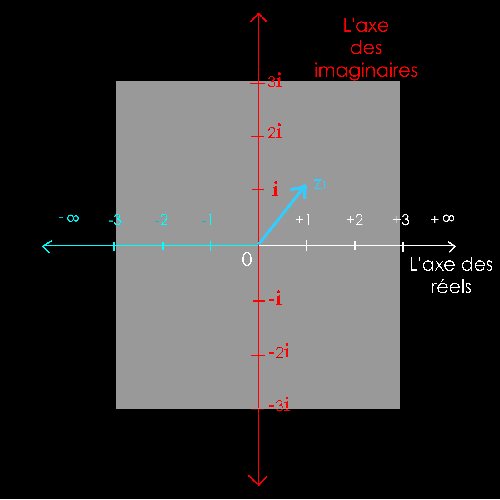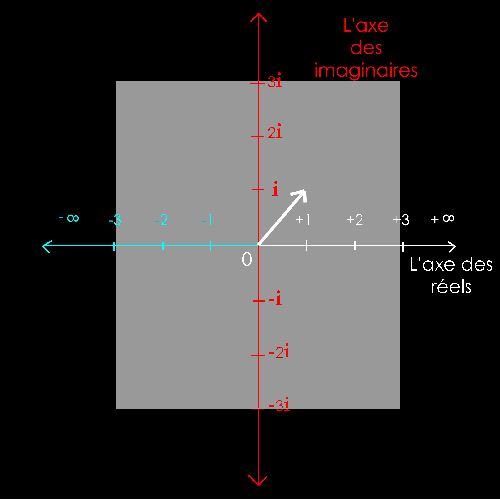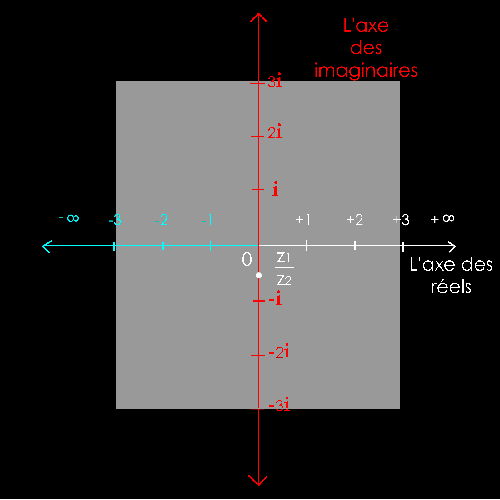
Soit
2 nombres complexes :
z1 = + i = + 1i
z2
= + 2i
La
solution est purement graphique (à la règle et au compas).
Il
s'agit de mettre bout à bout les 2 vecteurs z1 et z2
pour trouver le
nombre
imaginaire z1+ z2.
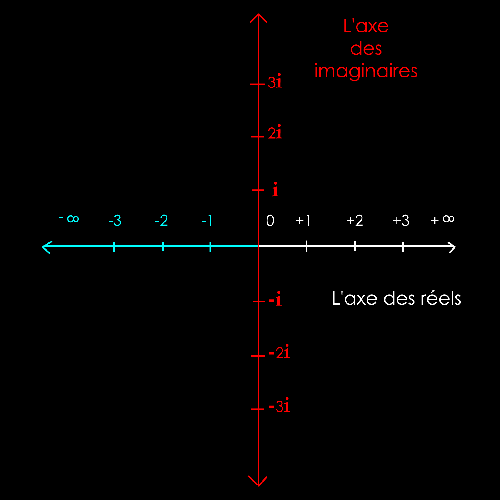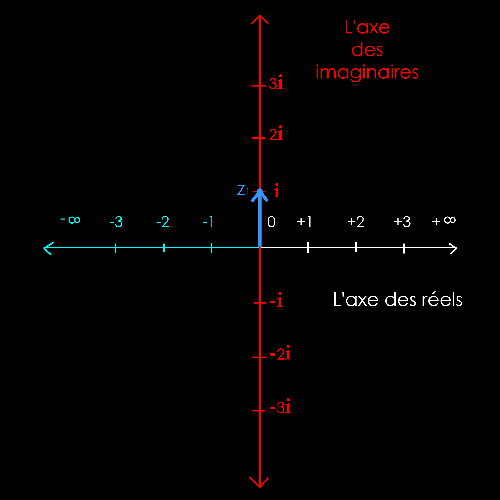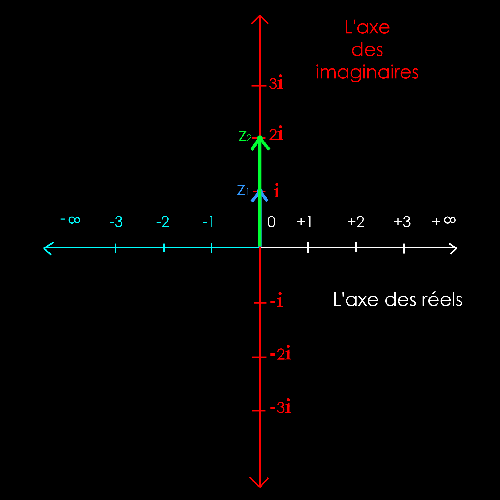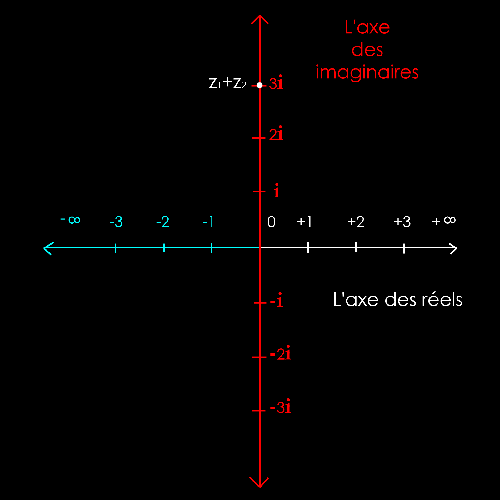

Soit
2 nombres complexes :
z1 = + i = + 1i
z2
= + 2i
La
solution est purement graphique (à la règle et au compas).
Il
s'agit de mettre bout à bout les 2 vecteurs z1 et
-
z2
pour trouver le
nombre
imaginaire z1-
z2.
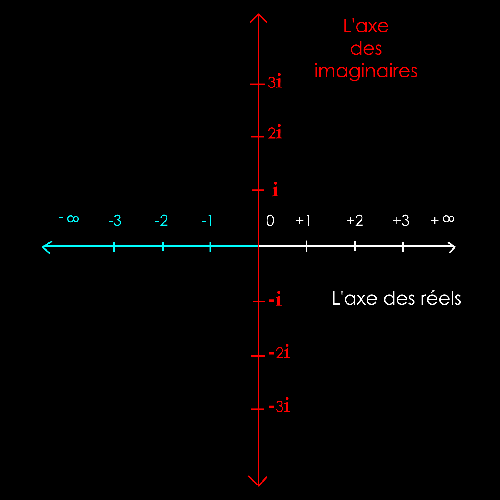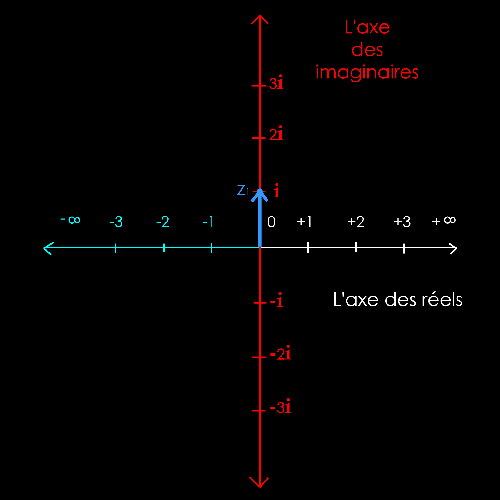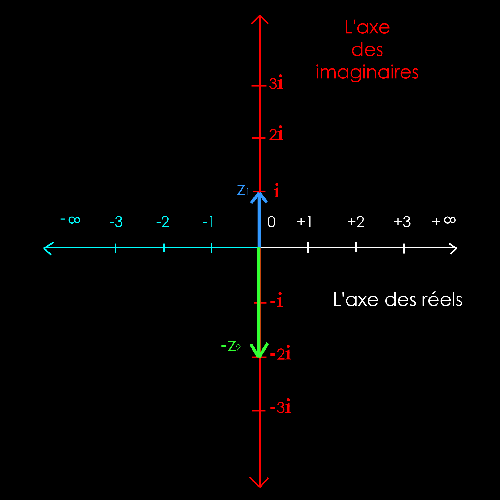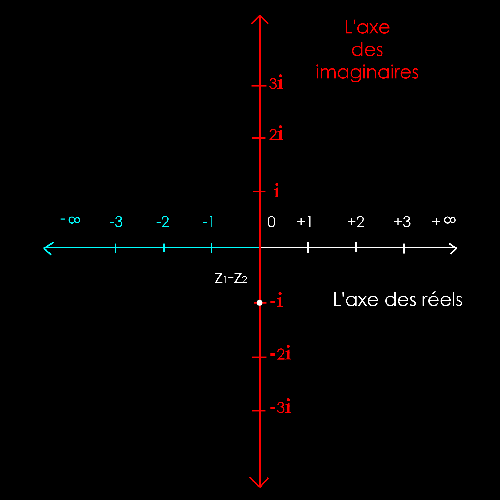

Soit
2 nombres complexes :
z1 = + i = + 1i
z2
= + 2i
La
solution graphique n’est possible qu’en passant par la forme trigonométrique.
z1
et z2 peuvent aussi s’écrirent :
![]()
![]()
Il
s'agit de dessiner le produit des 2 vecteurs z1 et z2
pour trouver le nombre complexe
z1
x
z2.
Multiplier 2 vecteurs,
c’est ajouter leur angles et multiplier leurs longueurs.
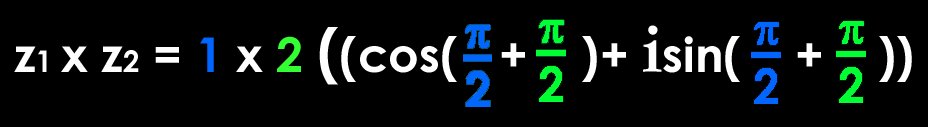
![]()
=
2
(- 1 + 0
)
=
- 2
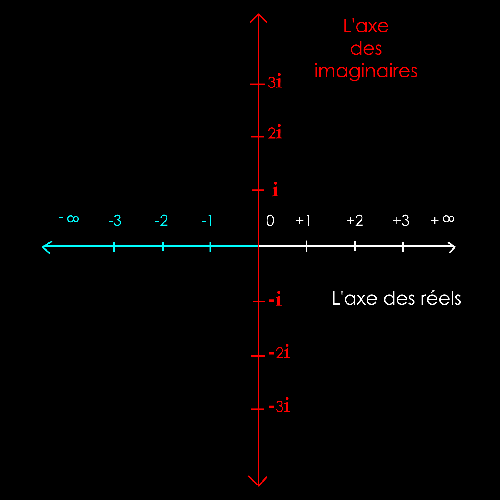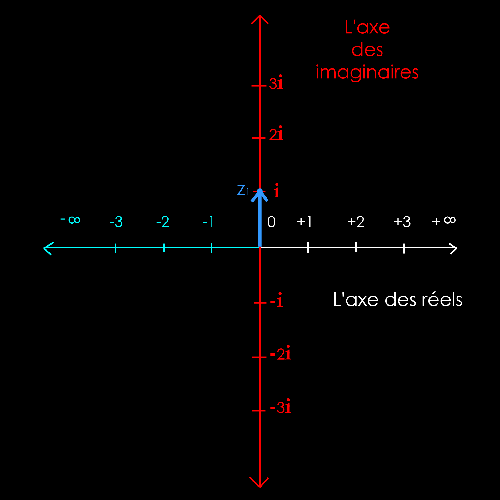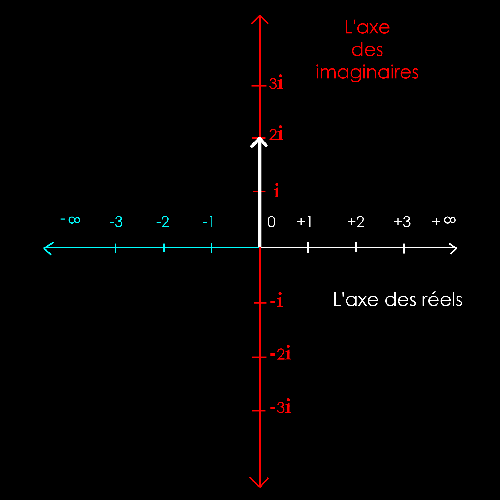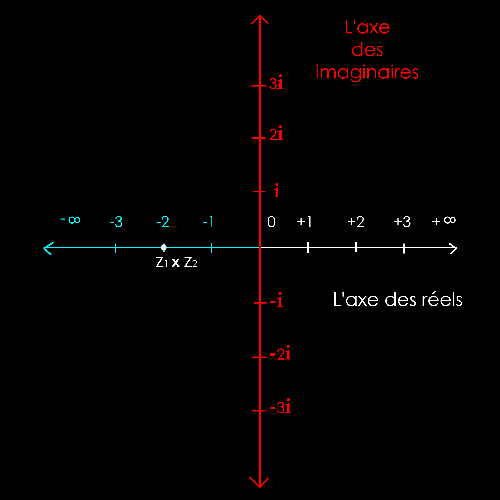

Soit
2 nombres complexes :
z1 = + i = + 1i
z2
= + 2i
La
solution graphique n’est possible qu’en passant par la forme trigonométrique.
z1
et z2 peuvent aussi s’écrirent :
![]()
![]()
Il s'agit de dessiner le produit des 2 vecteurs z1 et z2 pour trouver le nombre complexe :
![]()
Diviser 2 vecteurs, c’est
soustraire leur angles et diviser leurs longueurs.
![]()
![]()

![]()
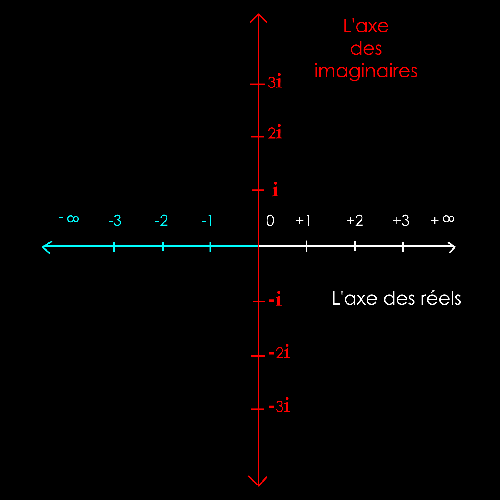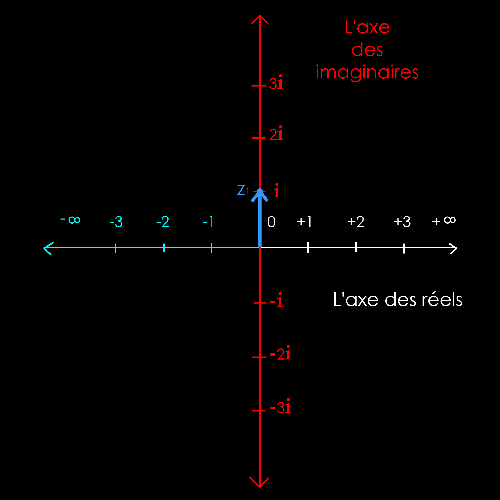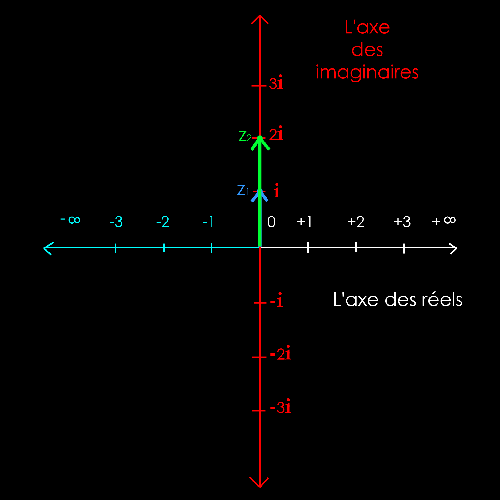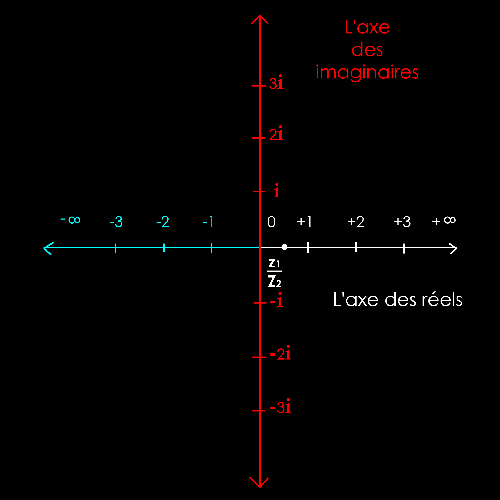


Soit
2 nombres complexes :
z1 = 1 + i = 1 + 1i
z2
= - 2 + 2i
La
solution est purement graphique (à la règle et au compas).
Il
s'agit de dessiner la somme des 2 vecteurs z1 et z2
pour trouver le
nombre
complexe z1+ z2.
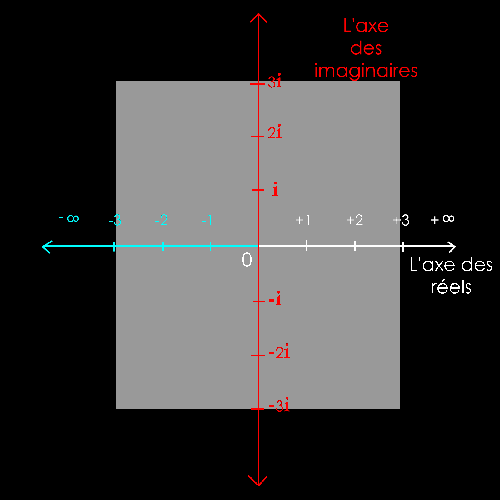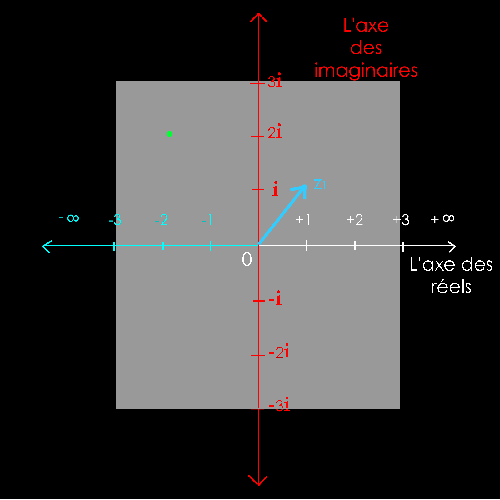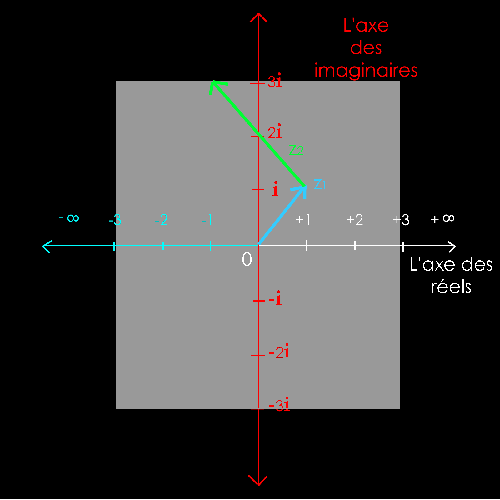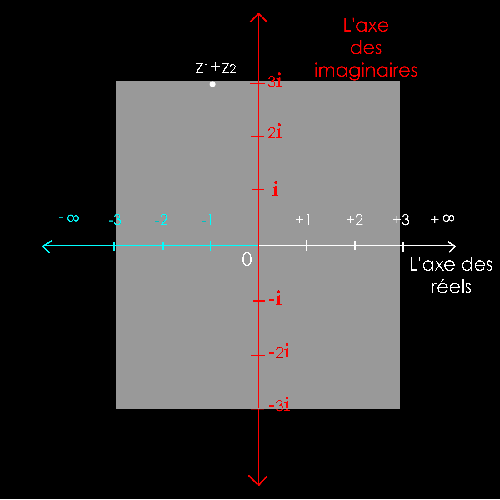

Soit
2 nombres complexes :
z1 = 1 + i = 1 + 1i
z2
= - 2 + 2i
La
solution est purement graphique (à la règle et au compas).
Il
s'agit de dessiner la somme des 2 vecteurs z1 et -z2
pour trouver le
nombre
complexe z1-z2.
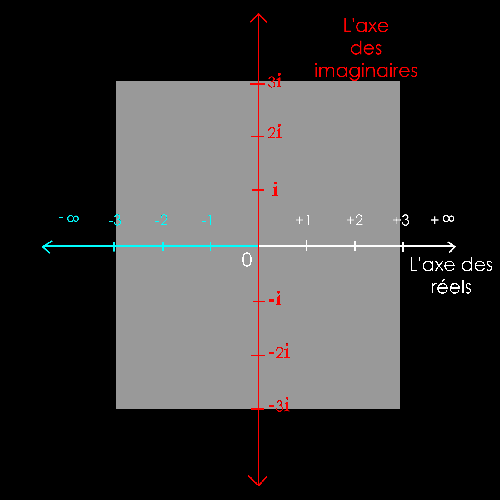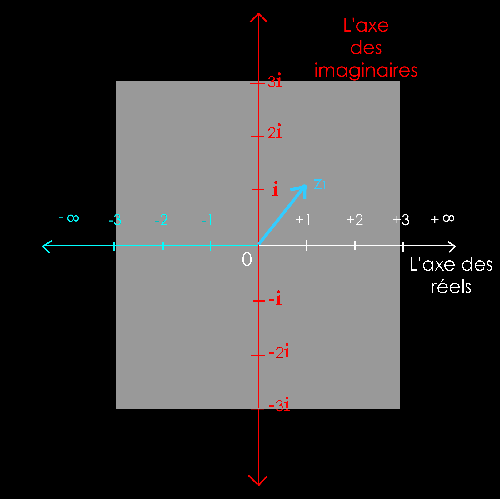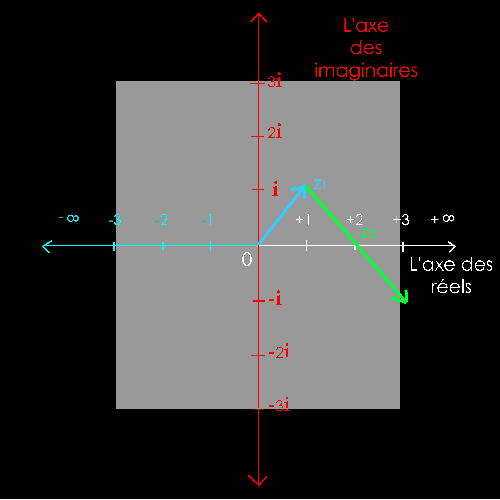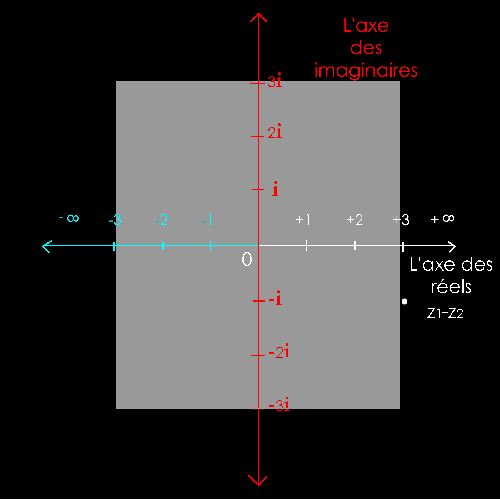

Soit
2 nombres complexes :
z1 = 1 + i = 1 + 1i
z2
= - 2 + 2i
La
solution graphique n’est possible qu’en passant par la forme trigonométrique.
z1
et z2 peuvent aussi s’écrirent :
![]()
![]()
Il
s'agit de dessiner le produit des 2 vecteurs z1 et z2
pour trouver le nombre complexe
z1
x
z2.
Multiplier 2 vecteurs,
c’est ajouter leur angles et multiplier leurs longueurs.
![]()
=
4 (cos![]() + i
sin
+ i
sin![]() )
)
=
4 (- 1 + 0i
)
= -
4
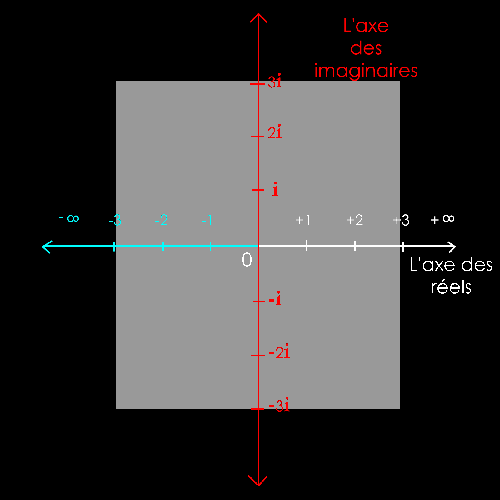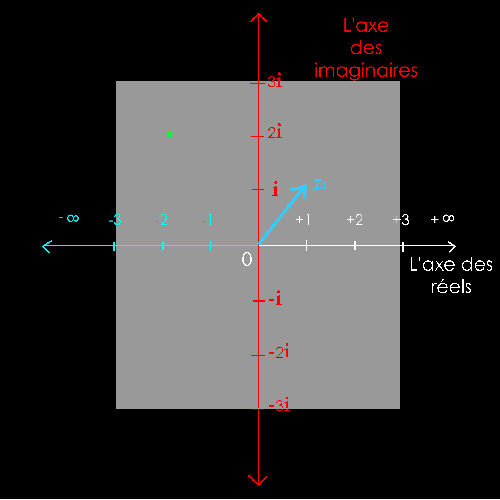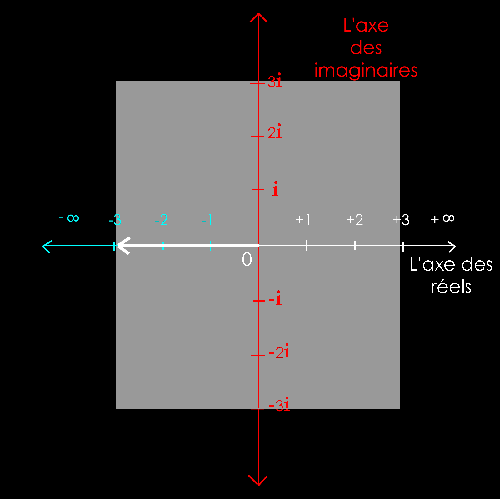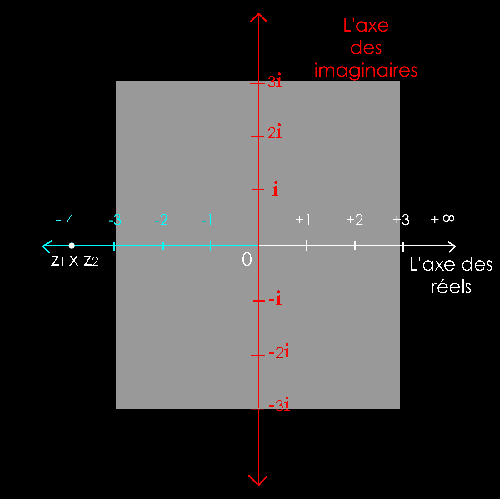

Soit
2 nombres complexes :
z1 = 1 + i = 1 + 1i
z2
= - 2 + 2i
La
solution graphique n’est possible qu’en passant par la forme trigonométrique.
z1
et z2 peuvent aussi s’écrirent :
![]()
![]()
Il s'agit de dessiner le produit des 2 vecteurs z1 et z2 pour trouver le nombre complexe :
![]()
Multiplier 2 vecteurs,
c’est soustraire leur angles et diviser leurs longueurs.
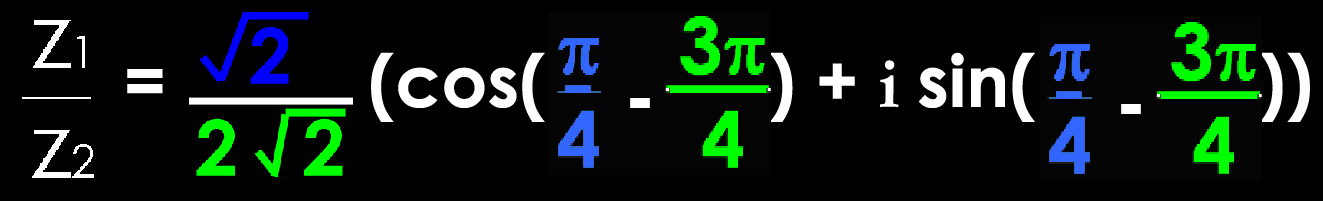
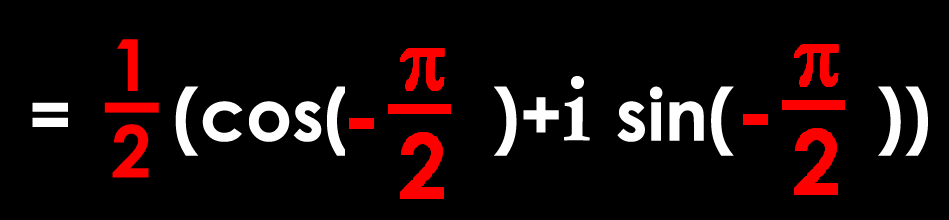
![]()
![]()